Dízimas periódicas Simples e Composta

As dízimas periódicas são números decimais periódicos, ou seja, apresentam um ou mais algarismos que se repetem na mesma ordem infinitamente. O algarismo que se repete é chamado de período.
Os números decimais periódicos pertencem ao conjunto dos números racionais, pois podem ser escritos na forma de fração. 
Quando um número é decimal infinito, mas não apresenta algarismos que se repetem, ou seja, não possui um período, ele não será uma dízima periódica e sim um número irracional.
Existe dois tipos de dízimas periódicas, vamos conhecer a primeira:

Dízima periódica simples

Dízima periódica simples é quando analisamos a parte decimal (parte depois da vírgula) e observamos que antes do período não aparece nenhum número diferente dele. Veja os exemplos:

a)1,4444... ( analisando a parte decimal podemos notar que antes do período 4,não aparece nenhum número diferente dele).

b)3,7777... ( analisando a parte decimal podemos notar que antes do período 7,não aparece nenhum número diferente dele).

Dízima periódica composta

Dízima periódica composta é quando analisamos a parte decimal (parte depois da vírgula) e observamos que antes do período aparece um número que é diferente dele. Veja os exemplos:

a)4,27777... (analisando a parte decimal podemos notar que antes do período 7 aparece um número diferente, no caso o número 2).

b)0,25323232... (analisando a parte decimal podemos notar que antes do período 32 aparece um número diferente, no caso o número 25).

 

Representação das dízimas periódicas

As dízimas podem estar escritas na forma de fração geratriz ou na forma de número decimal. Quando estiver escrita na forma decimal, colocamos três pontinhos no final para indicar que os algarismos se repetem infinitamente. Podemos ainda representar esse tipo de número colocando um traço horizontal apenas em cima do seu período.
Exemplos:

COMO SABER SE UMA DÍZIMA PERIÓDICA É SIMPLES OU COMPOSTA 

Exercício : Classifique em Dízima Periódica Simples ou Dízima Periódica Composta

a) 2,7777.... ►

b) 5,24444.... ►

c) 9,22222.... ►

d) 25,128888...►

e) 8,525252... ►

FRAÇÃO GERATRIZ DE UMA DÍZIMA PERIÓDICA

É possível determinar a fração que deu origem a uma dízima periódica.

Denominamos esta fração de geratriz da dízima periódica.

Assista a aula do Prof. Nivaldo Galvão e aprenda a encontrar a fração geratriz de um dízima periódica simples e composta.

 

EXERCÍCIOS

1) Analise a fração a seguir:

Podemos afirmar que ela é a fração geratriz da dízima:

A) 2,77…

B) 0,62626262…

C) 2,55…

D) 0,2666…

E) 0,27272727…

2) Seja x = 1,123123… A diferença entre o numerador e o denominador da sua representação fracionária é:

A) 123.

B) 999.

C) 321.

D) 112.

E)1122.

3) A fração geratriz de dízima periódica 3,151515… é igual a:

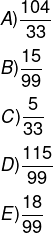
4) A fração geratriz da dízima 15,2222… é ?

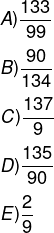
5) Assinale a alternativa que corresponde a fração geratriz da dízima periódica 2,5303030... 

a) 25/ 99

b) 37/ 9

c) 135/999

d) 267/990

e) 167/66