Razão

Resolução:
- número de cadeiras reservadas (17)
- número total de cadeiras (70)
Agora tente fazer as atividades abaixo:
1) (UERJ 2020) Admita que, em dezembro de 2014, uma filha tinha 20 anos e seu pai, 50.
Em dezembro de 2024, a razão entre as idades da filha e do pai será de:
A) 1/5
B) 1/2
C) 3/4
D) 4/3
A) 3/4
B) 2/3
C) 3/7
D) 2/5
E) 1/2
A → 28 quilômetros com 4 litros
B → 100 quilômetros com 14 litros
C → 60 quilômetros com 8 litros
D → 72 quilômetros com 9 litros
E → 84 quilômetros com 12 litros.
Sabendo que ele comprou o carro mais econômico, o escolhido foi?
A) A
B) B
C) C
D) D
E) E
4) Em uma sala de aula há 35 alunos, e 20 são meninas. A razão entre a quantidade de meninos e a quantidade de meninas é:
A) 4/7
B) 3/7
C) 1/2
D) 3/4
E) 4/3
5) Em um campeonato de futebol, a média de gols marcados por um time é muito importante para a análise do comportamento desse time e busca de melhorias no desempenho da equipe. Se um determinado clube marcou 12 vezes durante 20 jogos, podemos afirmar que a média de gols por partida é de:
A) 0,6 gol por partida.
B) 0,8 gol por partida.
C) 1 gol por partida.
D) 1,6 gol por partida.
E) 2 gols por partida.
6) Num exame,havia 180 candidatos,tendo sido aprovados 60,a razão entre o número de reprovados e o de aprovados é de:
a) 1/2
b) 2
c) 1/3
d) 3
7) Numa prova de Matemática,um aluno acertou 12 das 20 questões dadas.Qual é a razão do número de questões que ele acertou para o número de questões da prova?
a) 2/5
b) 3/5
c) 4/5
d) 2
8) Uma equipe de futebol apresenta o seguinte retrospecto no campeonato:
- 30 vitórias
- 18 empates
- 12 derrotas
Proporção
Os números racionais a, b, c e d são proporcionais se, e somente se, a igualdade a seguir for verdadeira.
![]()
De maneira equivalente, podemos dizer que a igualdade será verdadeira somente quando a multiplicação cruzada for verdadeira.Veja:
b . c = a . d
Como calcular proporções
Para verificar ou calcular se, de fato, os números são proporcionais, basta aplicar a primeira propriedade, caso a igualdade seja verdadeira, então os números são proporcionais. Veja os exemplos abaixo:
a)Verifique se os números 15, 30, 45 e 90 são proporcionais.
Devemos, nessa ordem, montar as razões e, em seguida, realizar a multiplicação cruzada.
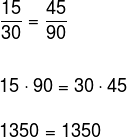
Conclusão: Como deu uma igualdade,os números nesta ordem formam uma proporção.
b) Os números 2, 4, x e 32 são proporcionais. Determine o valor de x.
Como afirmamos que os números, na ordem que foram apresentados, são proporcionais, logo, podemos igualar as razões entre eles e aplicar a propriedade fundamental, veja:

Exercício 1) Verifique se os números abaixo na ordem que eles aparecem são proporcionais:
a) 3 , 4 , 6 e 8
b) 4 , 8 , 10 e 20
c ) 7 , 3 , 49 e 21
d) 4 , 6 , 20 e 30
e) 8 , 9 , 10 e 15
f) 12 , 15 , 10 e 13
Exercício 2) Os números abaixo na ordem que eles aparecem são proporcionais,determine o valor de x:
a) 
b) .jpg)
c) .jpg)
Exercício 3) Uma criança de 1 m de altura projeta uma sombra de 0,5 m. No mesmo instante,um edifício de 18 m irá projetar uma sombra de :
a) 6 m
b) 8 m
c) 9 m
d) 12 m
Exercício 4) Uma fotografia tem 10 cm de largura e 15 cm de comprimento.Queremos ampliá-la de modo que seu comprimento tenha 18 cm.Então,na foto maior,a largura medirá:
a) 12 cm
b) 13 cm
c) 14 cm
d) 16 cm





































