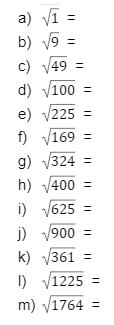Simetria de Translação

 O que acontece na Simetria de Translação?

Na simetria de translação, a figura "desliza" sobre uma reta, mantendo-se inalterada. Podemos citar como exemplo de translação, elevadores, escadas rolantes e até mesmo escorregadores.

Em todas as translações se observa que um mesmo elemento se desloca numa determinada direção e sempre paralelo a si próprio, isto é, sem nunca rodar.

Exemplos de aplicação da Simetria de Translação baseada em um vetor :

a)

Vetor com sentido para direita,com 7 unidades de comprimento e direção horizontal.

b) 

Vetor com sentido para direita,com 5 unidades de comprimento e direção com 1 unidade para baixo.

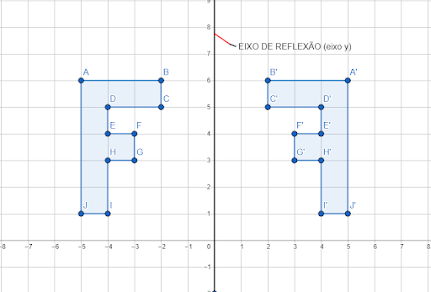
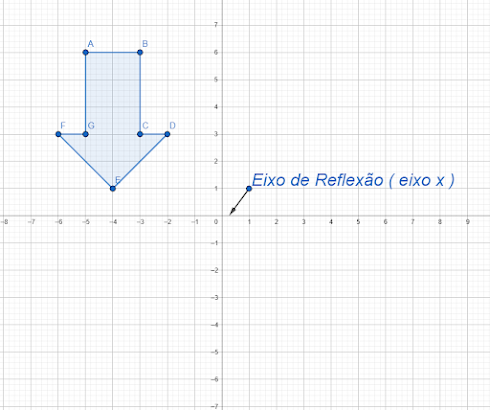
Simetria de Reflexão

Simetria de Reflexão ou Reflexiva

Na simetria de reflexão, também conhecida como do espelho ou axial, uma linha (eixo de reflexão) passa sobre a figura ou objeto de tal maneira que as duas partes ficam exatamente iguais, como se uma fosse uma o reflexo da outra.

A simetria de reflexão só acontece se as figuras/objetos obedecerem rigorosamente a mesma distância em relação ao eixo de reflexão.

Veja um exemplo:

Marque os pontos abaixo no Plano Cartesiano, depois ligue em ordem alfabética, não esqueça de ligar o ponto J com A :

A (-5;6)  B (-2;6)  C (-2;5)  D (-4;5)  E (-4;4)  F (-3;4)  G (-3;3)  H (-4;3)  

I (-4;1)   J (-5;1)

Exercício 1 - Nas figuras abaixo, aplique a Simetria de Reflexão e escreva as coordenadas da figura original e da sua reflexão:

a)

b) 

Exercício 2 -Escreva as coordenadas do quadrado que foi aplicada a simetria: 

    A' = (   ,    )     

    B' = (   ,    )          

    C' = (   ,    )            

    D' = (   ,    )

    E' = (   ,    )

   

Mais exercícios de simetria de reflexão

                                               

Simetria

 O que é Simetria?

Quando algo pode ser dividido em duas partes iguais, dizemos que é simétrico, ou seja, que tem simetria. Esse conceito é utilizado na geometria, na arte e até em nosso cotidiano ou na natureza.

Exemplo de Simetria na Natureza:

Exemplo de Simetria na Arte:

Exemplos de Simetria na Geometria:

Exemplos de Simetria na Arquitetura:

Exercício 1- Quantos e quais são os eixos de simetria das figuras abaixo:

a) Face do tigre:

b) Face da coruja:

c) Campo de futebol:

d) Triângulo Isósceles (2 lados iguais)

e) Pentágono regular (lados e ângulos iguais):

Dica: Quando o Polígono é regular (possui lados e ângulos iguais) o número de eixos de simetria é igual ao número de lados do polígono.

f) Hexágono regular (lados e ângulos iguais):

g) Octógono regular (lados e ângulos iguais):

h) Desenho de um coração:

Mais exercícios na plataforma do Khan Academy:

Como calcular raízes exatas

Nomenclatura:

Como calcular raiz quadrada

No exemplo acima o índice é 2,então lemos raiz quadrada de 16.O índice 2 não é representado, mas é importante saber, pois ele que determina quantas vezes vamos multiplicar um mesmo número, de modo que o resultado seja o radicando.

1º) Como no caso da raiz quadrada o índice é 2,iremos fazer 2 quadradinhos e colocar o sinal da multiplicação no meio deles.

2º) "Chutamos" o número 12 e multiplicamos por ele mesmo, deu 144 como passou de 81 é um aviso que "chutamos" um número alto.

3º) No segundo chute abaixamos para 8,deu menos que 81,agora "chutamos" um número baixo.

4º) Quando "chutamos" o 9 ,encontramos o radicando 81.

Veja:

Outro exemplo :

Calcule:

Como calcular raiz cúbica

No caso da raiz cúbica o índice é 3,logo para efetuar o cálculo, iremos fazer 3 quadradinhos e colocar dentro deles 3 números iguais que multiplicados resulta no radicando.

Veja um exemplo:

Calcule:

Veja no vídeo abaixo o cálculo de raiz quarta e raiz quinta:

Calcule:

Potenciação de Números Naturais

 Potenciação de Números Naturais

Casos especiais de potenciação:

Agora é com você:

Observando a tabela podemos notar dois casos especiais:

1º caso: Quando o expoente for 1,a potência é igual a própria base. (ver a penúltima linha da tabela)

2º caso: Todo número (com exceção do zero) elevado ao expoente zero é igual a 1. ( ver a última linha da tabela)

Exercício 1 - Calcule as potências:

Exercício 2 - Quiz de Potenciação:

Sistema Numeração Romano

 Números Romanos

Os números romanos foram o sistema de algarismos mais utilizado na Europa durante o Império Romano, antes de ser substituído pelos algarismos indo-arábicos, sistema que utilizamos atualmente. O sistema romano tinha como símbolos sete letras do alfabeto.

I → 1

V → 5

X → 10

L→ 50

C→ 100

D → 500

M → 1000

Os demais números são descritos pela repetição desses símbolos, levando-se em consideração que também existem regras específicas, a depender da posição dos seus algarismos. Ainda podemos ver algumas representações em números romanos, por exemplos, os séculos e tópicos de uma determinada lei, nos relógios, monumentos, representação das estações da Via – Sacra, capítulos de livros, nomear Papas.

•Regras dos números romanos

Utilizando os sete símbolos, podemos representar vários números no sistema de algarismos romanos, mas, para isso, é necessário respeitar algumas regras relativas ao valor posicional do símbolo.

Para representar números utilizando a combinação de símbolos, quando temos uma letra maior à esquerda (ou seja, escrevemos da maior para a menor letra) ou quando temos a repetição de um mesmo símbolo, faz-se a adição:

Exemplos:

a) III = 1 + 1 + 1 = 3

b) VI = 5 + 1 = 6

•Para realizar-se a soma, um símbolo pode ser repetido até três vezes. Na numeração romana, não se usa o símbolo em sequência quatro vezes para fazer-se somas. A exceção é o símbolo D, que representa 500, como se tem um símbolo para representar 1000, que é o M, o algarismo D nunca aparecerá duas vezes em um número.

Agora, quando representamos um algarismo menor à esquerda de um algarismo maior, nesse caso, realizamos a subtração entre eles.

Exemplos:

a) IV = 5 – 1 = 4

b) IX = 10 – 1 = 9

•O algarismo I só pode ser utilizado antecedendo V ou X, e não utilizamos repetições dele nesse caso. Por exemplo, para representar o 3, utilizamos III.

•Utilizando a mesma ideia, a letra X pode anteceder o L e o C como subtração, tornando possível a representação de números como:

XL → 50 – 10 = 40

•Não existem representações do tipo LC, o que, usando essa lógica, corresponderia a 100 – 50. O número 50 é representado por L, como vimos, então essa representação não faria sentido, por isso o L nunca será utilizado antes de uma letra que represente quantidades maiores.

A letra C pode ser utilizada antecedendo as letras D e M, tornando possível a representação de números como:

CD → 500 – 100 = 400

•Utilizando essas regras anteriores, o maior número que pode ser formado é 3999 (MMMCMXCIX), pois não se utiliza a sequência de quatro símbolos repetidos no sistema romano, porém, para representar números maiores, utiliza-se uma barra acima do algarismo:

Exemplos:

Representação de anos em Números Romanos

Representação de Números Romanos até 30

Representação de séculos em Números Romanos

Aprenda mais sobre Números Romanos com o Prof. Nivaldo Galvão

Atividades :

3. Observe as imagens e reescreva usando nosso sistema de Numeração Decimal:

4. Dê a resposta em Números Romanos :

a) O ano do descobrimento do Brasil ►

b) Papa João 23 ►

c) Século 18 ►

d) Capítulo 5 ►

e) 4 mil►

f) 2020 foi um ano difícil►

g) 3500►

h) A cidade de São Paulo foi fundada em 25 de janeiro de 1554 ►

i) O Pico da Neblina tem 2995 metros de altura ►

j) O Pico da Bandeira tem 2900 metros de altura ►

k)A Pedra da Mina tem 2800 metros de altura ►

l) 5 000►

m) 6 450►

n) 8 520 ►