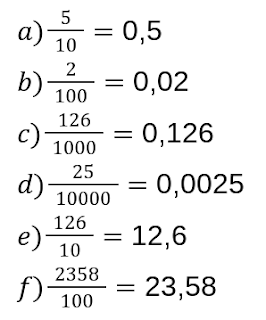Sequências Numéricas

Sequência numérica é a ação de dar continuidade a algo que já foi definido previamente, obedecendo uma determinada ordem. Quando estudamos sequências é importante descobrir regularidades, para determinar seus termos faltantes ou futuros. Uma sequência numérica deve ser representada entre parênteses e ordenada.

Exemplos: (1, 2, 3, 4, 5, 6, …): sequência dos números naturais;

(2, 3, 5, 7, 11, 13, 17, 19, …): sequência dos números primos positivos;

(1, 3, 5, 7, 9, …): sequência dos números ímpares positivos;

•Sequências recursivas

Quando determinado termo pode ser calculado em função de termos antecessores, ou seja, quando o termo seguinte depende do termo anterior.

Por exemplo, na sequência (2, 4, 6, 8, …) podemos observar que se trata da sequência dos números pares, portanto, devemos somar dois ao termo anterior para encontrar o próximo, nesse caso, o padrão dessa sequência corresponde a sempre adicionar o 2 para escrevê-la.

Nós também podemos realizar uma subtração como padrão(sempre subtrair 5) numa sequência, veja:

20, 15, 10 , 5 ,… (O quinto termo da sequência será o zero)

Atividade - Observe as sequências abaixo, descubra o padrão e escreva os três próximos termos:

a) 3, 6, 9, 12 …

Padrão:

Os três próximos termos:

b) 0, 10, 20, 30, 40, …

Padrão:

Os três próximos termos:

c) 18, 15, 12, …

Padrão:

Os três próximos termos:

d) 36, 32, 28, …

Padrão:

Os três próximos termos:

•Sequências não recursivas

As sequências não recursivas são aquelas que não dependem de termos anteriores para determinarmos o próximo termo, pode-se determinar o valor de um elemento da sequência apenas pela sua posição.
Por exemplo, na sequência (7,14,21,28...) não é necessário saber o último termo para determinar o seguinte. Observando atentamente, essa sequência é formada pelos múltiplos de 7.Já no caso da sequência (2,3,5,7,11...)left parenthesis, 2, comma, 3, comma, 5, comma, 7, comma, 11, point, point, point, right parenthesis olhando atentamente, percebe-se que ela é formada pelos números primos.

Lei de formação de uma sequência numérica

A lei de formação é a regra que estabelece a formação dos termos de uma sequência numérica. A partir da lei de formação é possível obter qualquer termo da sequência numérica.

A lei de formação de uma sequência numérica também é conhecida como fórmula do termo geral.

Vamos adotar a letra n para indicar o número da posição do termo na sequência.

Exemplo 1: Qual o termo que vai ocupar a 15ª posição na sequência (2,5,8,11...)?

Exemplo 2: O termo 36 da sequência 2,9,16,23,... é:

a) -15

b) 247

c) 275

d) -36

Exemplo 3: Analise a sequência (4, 7, 10, 13, 16, ...). Sendo n um número natural que indica a posição de cada termo, qual lei de formação que os seus termos obedecem?

a) 2n + 1

b) 3n

c) 3n + 1

d) 3n - 1

Exemplo 4: Observe as figuras formadas por quadradinhos:

A 25ª figura terá :

a) 36 quadradinhos

b) 45 quadradinhos

c) 50 quadradinhos

d) 52 quadradinhos

EXERCÍCIOS

2. Observe a sequência formada por palitos de fósforo.

a) Qual a expressão algébrica que relaciona a quantidade de palitos com a quantidade de triângulos?

b) Qual a quantidade de palitos necessária para construir 100 triângulos?

c) E para construir 177 triângulos, quantos palitos são necessários?

3. Observe a sequência formada por bolinhas:

A figura que ocupará a 100ª posição terá quantas bolinhas?

Páginas

Como transformar Número Decimal em Fração Decimal

Como transformar Frações Decimais em Números Decimais

Frações Decimais

Agora vamos aprender a transformar uma fração decimal em um número decimal.