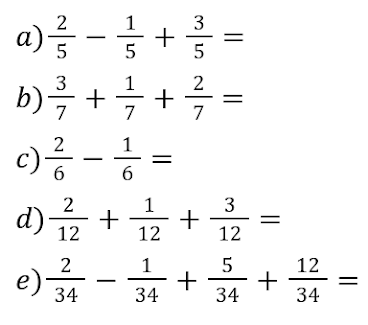Adição e Subtração de Frações

Adição e Subtração de Frações

1º caso: Os denominadores são iguais

Para calcular a adição ou subtração entre duas ou mais frações com denominadores iguais, conservamos o denominador e adicionamos ou  subtraímos os numeradores.

Exemplos : 

Observação : Existe casos que devemos simplificar o resultado dos cálculos:

Veja:

Veja como simplificar uma fração na videoaula abaixo:

@ngmatematica

SIMPLIFICAÇÃO DE FRAÇÕES

♬ som original - NG MATEMÁTICA

Exercício 1: O valor de

corresponde a :

a) 2/3

b) 1/8

c) 2/8

d) 1/2

Exercício 2: Calcule e simplifique se for necessário o resultado obtido:

 Exercício 3: O professor de Matemática passou uma lista de exercícios para que os alunos da turma de Eletrotécnica respondessem, em duplas, e entregassem uma semana depois. Cleiton e Bruno decidiram separar algumas questões para que fizessem separados e depois juntariam as respostas para que ganhassem tempo na resolução. Três dias depois, Cleiton conseguiu responder a 12/60 das questões, enquanto Bruno conseguiu resolver 18/60 das questões. Se eles não fizeram questões em comum, a fração da lista de exercícios respondida pela dupla Cleiton e Bruno é:

a) 2/3

b) 1/2

c) 2/5

d) 1/5

Exercício 4:Sandra comprou duas pizzas pequenas, uma de calabresa e a outra de queijo. Da primeira ela comeu 2/4 e da segunda conseguiu comer 1/4 . Que fração representa a quantidade total de pizzas que Sandra comeu, considerando que as pizzas possuem o mesmo tamanho?

Exercício 5:Um copo de leite fornece $\dfrac{3}{10}$start fraction, 3, divided by, 10, end fraction da quantidade de cálcio recomendada por dia.

$3$3 copos de leite fornecem que fração da quantidade de cálcio recomendada por dia?

Exercício 6:A tabela mostra a quantidade de bolo que $3$3 amigos comeram.

${}$	Quantidade comida
Thais	$\dfrac3{10}$start fraction, 3, divided by, 10, end fraction
Charles	$\dfrac5{10}$start fraction, 5, divided by, 10, end fraction
Catarina	$\dfrac1{10}$start fraction, 1, divided by, 10, end fraction

Qual a quantidade de bolo que os três comeram juntos?

2º caso: Os denominadores são diferentes

Nesse caso vamos aprender usando um método prático que tem a multiplicação como operação principal para resolver adição de frações.

Acompanhe o exemplo abaixo:

Veja passo a passo o que foi feito:

• Multiplicamos os denominadores entre si.
• Multiplicamos em forma de X.
• Somamos os 2 resultados obtidos (que estão dentro dos quadradinhos)
• Verificamos se é possível simplificar o resultado.

No caso da subtração de frações,o procedimento é o mesmo:

O que muda é que devemos subtrair os resultados obtidos quando multiplicamos em forma de X(números que estão dentro dos quadradinhos).

Exercício 1- Calcule , simplifique se for necessário e coloque a letra correspondente no quadro de respostas:

✔Quadro de respostas

Veja como fica o cálculo com mais de 2 frações:

Exercício 2- Calcule , simplifique se for necessário e coloque a letra correspondente no quadro de respostas:

✔Quadro de respostas

Soma e Subtração de Frações Negativas

 Soma de Frações Negativas

Subtração de Frações Negativas

@ngmatematica #subtraçãodefrações #fraçõesnegativas #fraçoes #fractions #fraçãomatematica ♬ som original NG MATEMÁTICA

Multiplicação de Números Inteiros - Conjunto Z

 Multiplicação de Números Inteiros 

A criação dos números inteiros foi um grande passo dado pela Matemática durante a sua evolução, eles surgiram da intensificação do comércio e da indústria, pois era necessário demonstrar situações de lucro e prejuízo nas operações comerciais e financeiras. Onde usavam números positivos, eram relacionados ao lucro e o número negativo era relacionado ao prejuízo.

Nesse conjunto, cada número inteiro positivo possui sua representação negativa,que são chamados de números opostos ou simétricos (exemplo: 5 e -5).

Na multiplicação de números inteiros, devemos seguir algumas condições de acordo com o sinal dos números. 

Os números envolvidos são chamados de fatores e o resultado é chamado de produto.

No cálculo do produto,devemos ficar atentos no sinal correto, para aprender como determinar esse sinal,assista a videoaula do Prof.Nivaldo Galvão.

@ngmatematica #multiplicação #inteiros #negative #numeros #números #positivos ♬ som original - NG MATEMÁTICA

Conclusão da regra de sinais da Multiplicação 

1) Calcule os produtos:

     a) (-114).(+2).(-5) = 

    b) (+4).(-25).(-351)=

    c) (-99).(-125).(-4).(+2)=

    d) (+9).(+1).(+2).(+5)=

    e) (-100).(-50).(-40).(-10)=

    f) (-12).(-100).(+30).(-1)=

    g) (-7).(+11).(-3)=

    h) (-2).(-14).(-5)=

    i) (-5).(+3)=

    j) (+8).(-9).0.(-16).(+18)=

   k) (-12).(+3).(+1)=

    l) (+1).(-101).(-10)=

    m) (+1).(+1).(+1).(+1)=

    n) (-1).(-1).(+135)=

    o) (-2).(-5).(+4)=

    p) (+6).(-3).(+2)=

    q) (-10).(-8).(+5)=

    r) (-12).(-5).(+4).(-1)=

2) Preencha as tabelas abaixo e responda qual jogador foi o vencedor no final das duas rodadas:

Fração de um Total

 Fração de um Total

Exercício 1.Para uma festa foram encomendados 750 doces, sendo 1/3 de brigadeiros. Quantos brigadeiros foram encomendados para a festa?

Exercício 2. Maria paga 600 reais de aluguel, o que corresponde a 1/5 do seu salário mensal. Quanto Maria ganha por mês?

 

Exercício 3. Uma encomenda levará 28 dias para ser entregue. Se já se passaram 5/7 do número de dias, quantos dias ainda faltam para a entrega da encomenda?

Exercício 4. Em uma empresa há um departamento com 6 funcionários casados. Esses funcionários representam 3/8 do total de funcionários do departamento. Quantos funcionários há nesse departamento?

Exercício 5. Um estádio de futebol tem capacidade máxima de 45.000 pessoas. Esse número corresponde a 9/10 da população de uma cidade. Quantos habitantes tem nessa cidade?

Simetria de Translação

 O que acontece na Simetria de Translação?

Na simetria de translação, a figura "desliza" sobre uma reta, mantendo-se inalterada. Podemos citar como exemplo de translação, elevadores, escadas rolantes e até mesmo escorregadores.

Em todas as translações se observa que um mesmo elemento se desloca numa determinada direção e sempre paralelo a si próprio, isto é, sem nunca rodar.

Exemplos de aplicação da Simetria de Translação baseada em um vetor :

a)

Vetor com sentido para direita,com 7 unidades de comprimento e direção horizontal.

b) 

Vetor com sentido para direita,com 5 unidades de comprimento e direção com 1 unidade para baixo.

Simetria de Reflexão

Simetria de Reflexão ou Reflexiva

Na simetria de reflexão, também conhecida como do espelho ou axial, uma linha (eixo de reflexão) passa sobre a figura ou objeto de tal maneira que as duas partes ficam exatamente iguais, como se uma fosse uma o reflexo da outra.

A simetria de reflexão só acontece se as figuras/objetos obedecerem rigorosamente a mesma distância em relação ao eixo de reflexão.

Veja um exemplo:

Marque os pontos abaixo no Plano Cartesiano, depois ligue em ordem alfabética, não esqueça de ligar o ponto J com A :

A (-5;6)  B (-2;6)  C (-2;5)  D (-4;5)  E (-4;4)  F (-3;4)  G (-3;3)  H (-4;3)  

I (-4;1)   J (-5;1)

Exercício 1 - Nas figuras abaixo, aplique a Simetria de Reflexão e escreva as coordenadas da figura original e da sua reflexão:

a)

b) 

Exercício 2 -Escreva as coordenadas do quadrado que foi aplicada a simetria: 

    A' = (   ,    )     

    B' = (   ,    )          

    C' = (   ,    )            

    D' = (   ,    )

    E' = (   ,    )

   

Mais exercícios de simetria de reflexão